Detecting Forged Bank Notes
Problem Description
Physical currencies, especially banknotes, are at risk of forgery. These forgeries continue to improve in accuracy due to new counterfeiting methods. By using specialized techniques, however, it is possible differentiate authentic banknotes from forgeries and thereby maintain their integrity. The authors Eugen and Lohweg discussed a methodology for classifying forgeries, and their relevant dataset was donated to the UCI Machine Learning repository. In this project, a neural network will be used to find a way of predicting if a bank note is forged or not by using this data.
Note: if you would like to test the code yourself and follow along with this post, run np.random.seed(700) so that you can reproduce the values calculated here. An additional benefit of negating randomness is that it prevents interference with output consistency once training begins.
import numpy as np
np.random.seed(700)
Dataset Summary
The dataset comprises of 1372 instances, with class labels of 0 or 1. The dataset does not give definitions for labels, so I take 0 to mean authentic and 1 to mean forged. Each instance has 4 input features: variance, skewness, curtosis, and entropy. According to the documentation on the Machine Learning repository, features were extracted by using a Wavelet Transform Tool. The original research paper from Gillich and Lohweg further states that the Wavelet Transform was used on a region of interest on a banknote, which was captured by an industrial camera in grayscale.
There are 762 instances of the class with label 0, and 610 instances of the class with label 1, which is a slight imbalance. Expressed as a percentage, class 0 is approximately 55% of the entire dataset, while class 1 is approximately 44%. The imbalance should not be significant enough to create a highly biased model.
Dataset Processing
Before the data can be used for training on a neural network, it must first be processed. Processing usually involves normalization, transposing (depending on how data will be read), and splitting of the original dataset into various sets. For this problem, rows will be used to store all features, and columns will represent individual examples. We’ll begin processing by loading the dataset into memory:
NOTES_FILE = "C:\\Users\\Shan\\Downloads\\data_banknote_authentication.txt"
banknote_data = np.genfromtxt(NOTES_FILE, delimiter=',')
The data is originally sorted by label and data is stored opposite to how it is needed, so the set has to be shuffled and transposed:
np.random.shuffle(banknote_data)
banknote_data = banknote_data.T
Normalization is necessary so that all input features can be given equal weight, otherwise the network may not learn properly. However, if the scales of each input feature are similar, it may not be necessary. A quick check of the data by using min and max will reveal if it’s necessary:
print(f'Min: {banknote_data.min(axis=1)} \n' \
f'Max: {banknote_data.max(axis=1)}')
The outputs are within similar ranges so it’s not necessary to normalize.
Min: [ -7.0421 -13.7731 -5.2861 -8.5482 0. ]
Max: [ 6.8248 12.9516 17.9274 2.4495 1. ]
Now, the dataset can be split. It will be divided into a training set, a validation set, and lastly a test set. The training set will be used for evaluating baseline performance and initial model creation, while the validation set will be used to monitor overfitting. The test set will be used only to measure performance of the fully tuned network.
The distribution of examples among sets will be 60%/20%/20%. The instances in the file are sorted by class, so the dataset has to be shuffled before splitting. The split won’t be perfectly distributed, so the final numbers are 823/274/275. Shuffling and splitting is achieved by the code below.
train_split = banknote_data[:, :823]
validation_split = banknote_data[:, 823:1097]
test_split = banknote_data[:, 1097:1372]
It’s also important to verify the label distributions aren’t too imbalanced. The code below can be used to do this:
def print_label_count(dataset_labels):
class_0_labels = np.count_nonzero(dataset_labels == 0)
class_1_labels = np.count_nonzero(dataset_labels == 1)
print(f'Class 0 labels: {class_0_labels}. Class 1 labels: {class_1_labels}. Total labels: {dataset_labels.shape[0]}')
print_label_count(train_split[-1, :])
print_label_count(validation_split[-1, :])
print_label_count(test_split[-1, :])
The split is fairly balanced among each set.
Class 0 labels: 464. Class 1 labels: 359. Total labels: 823
Class 0 labels: 151. Class 1 labels: 123. Total labels: 274
Class 0 labels: 147. Class 1 labels: 128. Total labels: 275
Network Architecture
This problem is a binary classification problem- it’s either an authentic banknote or forged, so a simple neural network can be used to solve it. To begin the experimentation process, the input layer will have 4 input neurons, one for each feature. The hidden layer was randomly selected to have 10 hidden features and will use ReLU activation. The output layer will have only one output neuron and will use Sigmoid activation since we’re expecting a single probability from the network. Finally, cross entropy will be used to calculate loss. A diagram is presented below:
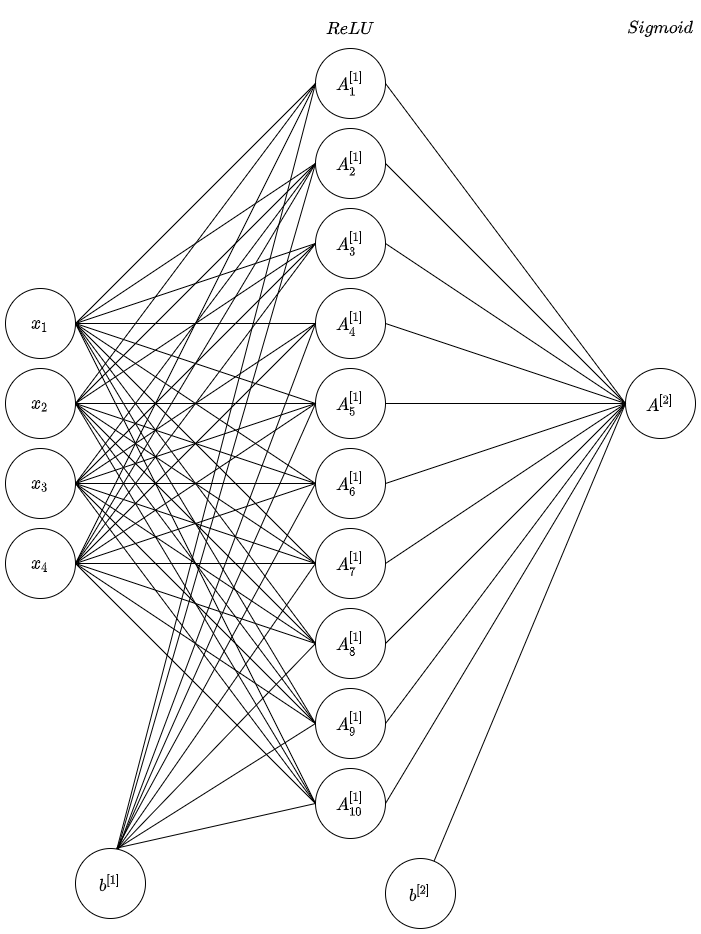
The main functions of the network are given below, and these functions have been vectorized to maximize performance. If you’re interested in finding out how the backpropagation equations were calculated for this network, you can find an explanation here.
def convert_split_to_xy(split):
Y = split[-1]
X = np.delete(split, (4), axis=0)
return (X, Y)
def initialize_coefficients(layers):
L = len(layers)
weights = [np.random.randn(layers[l], layers[l-1]) * 0.01 for l in range(1, L)]
biases = [np.zeros((layers[l], 1)) for l in range(1, L)]
return weights, biases
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def relu(x):
return np.maximum(0, x)
def relu_derivative(x):
x[x<=0] = 0
x[x>0] = 1
return x
def average_cross_entropy(Y, A, n):
cross_entropy = -(Y * np.log(A) + (1 - Y) * np.log(1 - A))
return 1/n * np.sum(cross_entropy)
def feed_forward(w, X, b, activation_fn):
Z = np.dot(w, X) + b
A = activation_fn(Z)
return (A, Z)
def forward_propagate(W, X, b):
A1, Z1 = feed_forward(W[0], X, b[0], relu)
A2, Z2 = feed_forward(W[1], A1, b[1], sigmoid)
return (A1, A2, Z1, Z2)
def backpropagate_2nd_layer(A1, A2, Y, n):
dL_dZ2 = A2 - Y
dL_dW2 = 1/n * np.dot(dL_dZ2, A1.T)
dL_dB2 = 1/n * dL_dZ2.sum(axis=1, keepdims=True)
return (dL_dZ2, dL_dW2, dL_dB2)
def backpropagate_1st_layer(W, X, dL_dZ2, Z1, n):
dL_dZ1 = np.dot(dL_dZ2.T, W[1]) * relu_derivative(Z1).T
dL_dW1 = 1/n * np.dot(dL_dZ1.T, X.T)
dL_dB1 = 1/n * dL_dZ1.sum(axis=0, keepdims=True).T
return (dL_dW1, dL_dB1)
def update_weights(alpha, gradients, W, b):
dL_dW1, dL_dW2, dL_dB1, dL_dB2 = gradients
W[0] -= alpha * dL_dW1
W[1] -= alpha * dL_dW2
b[0] -= alpha * dL_dB1
b[1] -= alpha * dL_dB2
def binarize(x):
return (x > 0.5).astype(np.float_)
def calculate_accuracy(A, Y):
A = binarize(A)
return np.equal(A, Y).sum() / Y.shape[0] * 100
def evaluate_performance(A, Y, dataset):
accuracy = calculate_accuracy(A, Y)
A = binarize(A)
result = np.equal(A, Y)
print(f'{dataset} accuracy: {accuracy}. {dataset} misclassifications: {A[np.where(result == False)]}')
The actual training of the network will be done by the following code. We’ll use the following arbitrary hyperparameters to start off with: 2500 epochs and a learning rate (alpha) of 0.0075. Weights will have the distribution $W \sim \mathcal{N}(0, 0.01)$ and biases will be set to zero.
Note: the graph generation code is omitted for the sake of brevity, but is available in the final repository- see the Resources section.
train_X, train_Y = convert_split_to_xy(train_split)
alpha = 0.0075
epochs = 2500
n = len(train_Y)
weights, biases = initialize_coefficients([4, 10, 1])
for i in range(epochs + 1):
train_A1, train_A2, train_Z1, _ = forward_propagate(weights, train_X, biases)
dL_dZ2, dL_dW2, dL_dB2 = backpropagate_2nd_layer(train_A1, train_A2, train_Y, n)
dL_dW1, dL_dB1 = backpropagate_1st_layer(weights, train_X, dL_dZ2, train_Z1, n)
gradients = (dL_dW1, dL_dW2, dL_dB1, dL_dB2)
update_weights(alpha, gradients, weights, biases)
if i == epochs:
evaluate_performance(train_A2, train_Y, 'Training')
evaluate_performance(validation_A2, validation_Y, 'Test')
Baseline Results
Running the above code produces the following graphs:
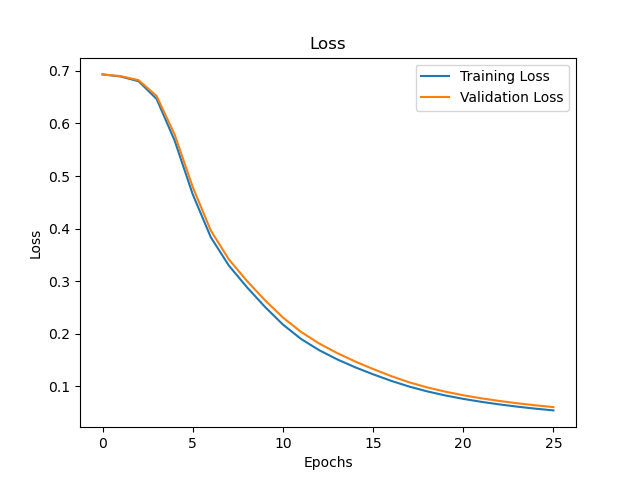
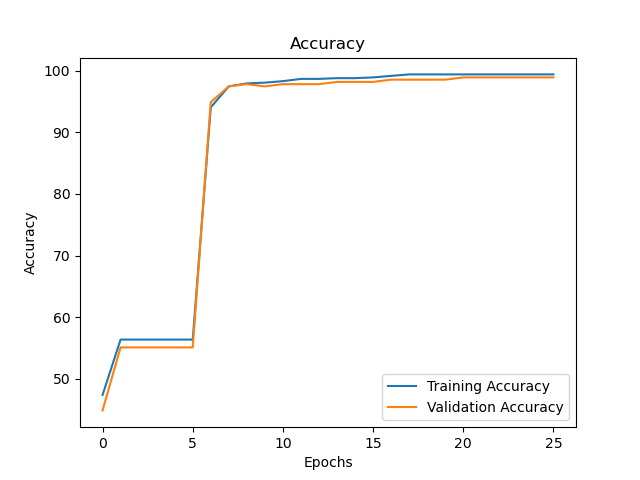
Although the accuracy for both datasets is good (99.39% and 98.9% respectively), accuracy alone does not give enough information on how well the model is performing. A confusion matrix can be created to show which classes are not being predicted correctly. This is the confusion matrix for the training set:
| n = 823 | Predicted: 0 | Predicted: 1 |
|---|---|---|
| Actual: 0 | 464 | 5 |
| Actual: 1 | 0 | 354 |
This is the confusion matrix for the validation set:
| n = 274 | Predicted: 0 | Predicted: 1 |
|---|---|---|
| Actual: 0 | 151 | 3 |
| Actual: 1 | 0 | 120 |
The confusion matrices show that the network has misclassified some authentic banknotes as forgeries (false positives). It is tempting to conclude that the class imbalance is the cause for the misclassifications, but this cannot be said for certain at this point. Other factors can explain this phenomena (e.g. the network hasn’t converged yet). Further improvements will be made to the network before definitive conclusions are made.
Improvements and Final Model
A simple improvement that can be made is using He Initialization, which is a weight initialization method described by He et al. in their 2015 paper. Usage of ReLU for non-output layer activations enables immediate usage of the method, and its usage will cause convergence to happen at a faster rate. It is given by setting the biases to 0, while setting the following distribution for weights:
\[W \sim \mathcal{N}(0, \sqrt{\frac{2}{n_l}})\]Changing the weight distributions and leaving all other hyperparameters unchanged produced 100% accuracy across the training and valdiation sets. This created some skepticism, which prompted me to verify my results by checking the original research paper. The authors of the original paper (Eugen and Lohweg) made use of a SVM, which was 100% accurate in its classification. Additionally, in the figures they produced (viz. Fig 6), the data was shown to have relatively simple decision boundaries.
As a result, I conclude that the network has converged and successfully approximated the decision boundary function. There is consequently no need for further improvements which were planned, such as regularization.
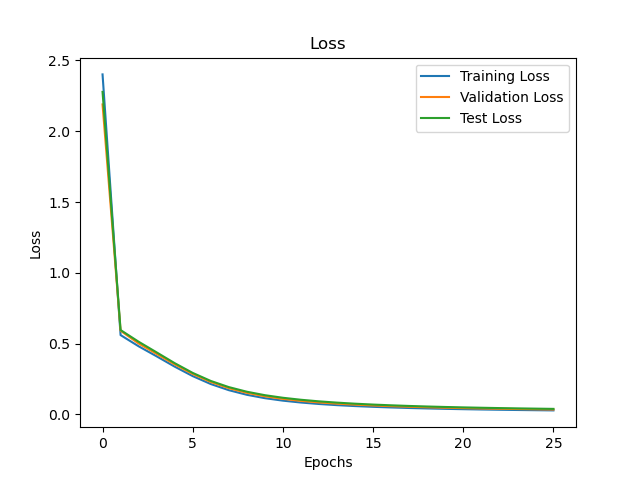
The final model was trained and tested across all 3 sets. All 3 sets had 100% accuracy, and the final training graphs are shown below.
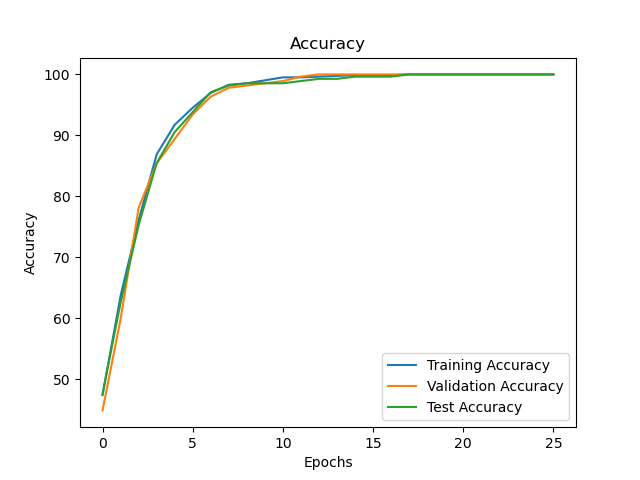
Extensions and Remarks
The code written here uses gradient descent. Although gradient descent has its advantages (e.g less noise during training), as a dataset grows in size, gradient descent becomes less feasible to use because it is time consuming on larger datasets. If the dataset becomes extremely large, a better option would be to use mini-batch gradient descent. Although it is noisier, it allows for faster training and therefore, faster model evaluation.
All the code for this project was written from scratch (i.e. without a framework). If this were a project given in a corporate environment, I’d advise against writing a neural network from scratch because of the time it can take to write to write the network itself, along with unit tests for all calculations. Frameworks have the advantage of having multiple techniques already coded and tested, which gives teams a lot more options when doing model evaluation. Additionally, well-maintained frameworks give long-term safety and reliability to a project that makes use of them. Much like standard software development, there’s no advantage to be gained from writing what is essentially boilerplate code.
Conclusion
This was a relatively simple dataset- a low number of input features and clear decision boundaries. As a result, it was possible to achieve perfect classification on this dataset with a straightforward and minimal approach. The integrity of the results was further proved by comparison to the results of the original authors. In the future, it may be possible to create cameras that can immediately calculate whether a banknote is forged or not by checking an ROI and thereafter calculating the network’s output by using a FPGA.
Resources
Citations
Dua, D. and Graff, C. (2019). UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science.
Gillich, Eugen & Lohweg, Volker. (2010). Banknote Authentication.
He, Zhang, Ren, and Sun. (2015). Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
